
Wie im Artikel zu den Grundlagen von Genetischen Algorithmen angekündigt, will ich in diesem Bereich noch ein paar weitere Artikel schreiben. Diesmal schauen wir uns das Thema Selektion an. Diese können auch unabhängig von Genetischen Algorithmen praktisch sein.
Inhaltsverzeichnis
Selektionsverfahren Allgemein
Bei den Selektionsverfahren werden zwei verschiedene Arten unterschieden: Natürliche Selektionsverfahren (Natural Selection) und Künstliche Selektionsverfahren (Artifical Selection)
Dies liegt daran, dass die Selektion von Individuen in zwei Schritten durchgeführt werden. Als erstes wird ein fitness abhängiger Erwartungswert festgelegt. Dabei handelt es sich um den Erwartungswert, wie viele Nachkommen das Individuum in der neuen Population haben wird. (Natrual Selection)
Im zweiten Schritt wird dann die eigentliche Auswahl der Individuen für die Reproduktion getroffen. (Artifical Selection)
Natürliche Selektion
Bei der Natürlichen Selektion werden im wesentliche drei Verfahren unterschieden:
- Fitness Proportional Selection
- Rank-Based Selection
Im Zuge eines Projektes an der Hochschule habe ich nur eines dieser drei Verfahren implementiert. Ich werde hier trotzdem alle drei Verfahren erklären.
Fitness Proportional Selection
Bei diesem Verfahren ist die Auswahlwahrscheinlichkeit ps(I) direkt proportional zur Fitness des einzelnen Individuum. Die passende Formel seht ihr in diese Bild.
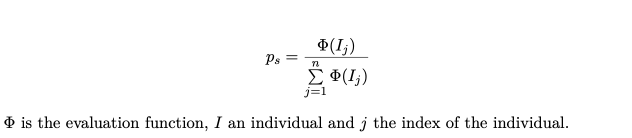
Der Selektionsdruck bei bei der Fitness Proportional Selection ist jedoch relativ gering. Je höher der Auswahldruck ist, desto schneller wird der Algorithmus konvergieren und ein lokales Optimum finden. Das heißt der genetische Algorithmus braucht weniger Durchläufe (Generationen) um das zugrundeliegende Problem zu lösen.
Eine Beispielimplementierung in C# sieht wie folgt aus:
1 2 3 4 5 | public void FitnessProportional(){ for (int i = 0; i < population.playerNum; i++){ population.Players[i].GetComponent<Player>().rating = population.Players[i].GetComponent<Player>().fitness; } } |
Rank-Based Selection
Bei dieser Selektionsvariante steht die Auswahlwahrscheinlichkeit ps nicht mehr in direktem Verhältnis zur Fitness. Stattdessen wurden die Individuen der Population absteigend nach Fitnesswert sortiert und nummeriert. Die Auswahlwahrscheinlichkeit hängt nun mit dem resultierenden Rang eines Individuum zusammen.
Künstliche Selektion
Bei der Künstlichen Selektion unterscheidet man im wesentlichen zwei unterschiedliche Verfahren:
- Roulette Principle
- Stochastic Universal Sampling
Roulette Principle
Das Roulette Prinzip kann man sich wie ein Roulette Rad vorstellen. Dieses Rad wird in n Abschnitte unterteilt. n ist dabei gleich der Populationsgröße.
Das Rouletterad wird in unterschiedliche große Bereiche unterteilt. Die größe der Bereiche ist direkt proportional zur Auswahlwahrscheinlichkeit des Individuum. Das heißt je höher die Fitness eines Individuums ist, desto wahrscheinlicher wird dieses Individuum selektiert.
Zum Selektieren wird eine Kugel in das Roulette Rad gelegt. Nachdem die Kugel in einen Abschnitt liegen geblieben ist, wird dieses Individuum in den Marting Pool überführt.
Um das ganze einfacher zu realisieren, wird die Fitness der einzelnen Individuen in einen Wert zwischen 0 und 1 umgerechnet. Die Implementierung in meinem Projekt sieht wie folgt aus:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | public void RoulettePrinciple(int num){ float fitSum = population.fitnessSum; for (int i = 0; i < population.playerNum; i++){ population.Players[i].GetComponent<Player>().relativeFitness = population.Players[i].GetComponent<Player>().rating / population.fitnessSum; } sorted = population.Players.ToList().OrderBy(relativeFitness => relativeFitness.GetComponent<Player>().relativeFitness).ToList().ToArray(); population.MartingPool = new GameObject [num]; int p = 0; while (p < num){ float r = Random.Range (0.0000f, 1.00000f)/4; int x = 0; while (x < population.playerNum){ if (r < sorted[x].GetComponent<Player>().relativeFitness){ population.MartingPool[p] = sorted[x]; p++; break; } x++; } } } |
Stochastic Universal Sampling
Beim Stochastic Universal Sampling (SUS) wird eine Art Glücksrad verwendet. Das Rad wird ebenfalls proportional zur Fitness eines Individuum eingeteilt. Zusätzlich werden n Zeiger in gleichmäßigen Abständen um das Rad verteilt.
Jetzt wird das Rad gedreht. Jedes Individuum auf den ein Zeiger gerichtet ist, wird in den Marting Pool überführt. Durch dieses Verfahren kann ausgeschlossen werden, dass n gleiche Individuen im Marting Pool vorkommen.
Meine Beispielimplementierung sieht wie folgt aus:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | public void StochasticUniversalSampling(int num){ for (int k = 0; k < population.playerNum; k++){ population.Players[k].GetComponent<Player>().relativeFitness = population.Players[k].GetComponent<Player>().rating; } sorted = population.Players.ToList().OrderBy(relativeFitness => relativeFitness.GetComponent<Player>().relativeFitness).ToList().ToArray(); float fitSum = population.fitnessSum; float pointDistance = fitSum / num; float r = Random.Range (0.0000f, sorted[0].GetComponent<Player>().relativeFitness) * pointDistance; population.MartingPool = new GameObject [num]; int i = 0; float sum = sorted[i].GetComponent<Player>().relativeFitness; for (int j = 0; j < num; j++){ float pointer = r + j * pointDistance; if (sum >= pointer){ population.MartingPool[j] = sorted[i]; } else { for(++i; i < population.playerNum;i++ ){ sum += sorted[i].GetComponent<Player>().relativeFitness; if( sum >= pointer){ population.MartingPool[j] = sorted[i]; break; } } } } } |
Um das ganze etwas zu Illustrieren, hier eine Grafik von Maik Buttelmann und Boris Lohmann
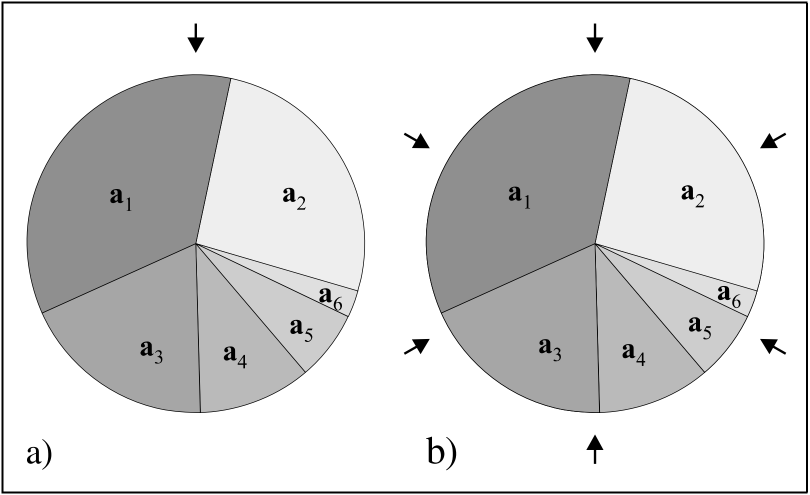
Damit haben wir den Einstieg in das Thema Selektionsverfahren abgeschlossen.
Falls ihr das ganze mal testen wollt, könnt ihr euch einfach das Unity 3D Projekt dazu von GitHub klonen.
Schreibe einen Kommentar